
Zielgruppe: Zyklen 3-4
Fokus: Durch Sachaufgaben zum arithmetischen Verständnis
Lehrperson: Jacques Kieffer
Schule: EF Schoulkauz, Zyklus 3.1
Um den Schüler/-innen mathematisches Verständnis zu ermöglichen, ist es wichtig, dass ihnen die Möglichkeit gegeben wird, Bilder und Repräsentationen entstehen zu lassen. Deshalb ist der reale Bezug von Bedeutung, welcher mit Hilfe von Sachaufgaben Gegenstand des Lernens wird.
Contexte
Im Anschluss an die Bearbeitung des Einmaleins lernen die Schüler/-innen die Division als Umkehraufgaben kennen. Zudem will ich auch die Divisionsaufgaben mit Rest einführen. Aus dem Grund, dass die Schüler/-innen zunächst keinen Bezug zu solchen arithmetischen Aufgaben herstellen können, habe ich mich dafür entschieden die Thematik anhand von Sachaufgaben einzuführen, welche zum großen Teil einen Bezug zum Alltag der Schüler/-innen nehmen.
Objectifs
Sachrechnen – die Fragestellung einer Sachaufgabe untersuchen und einen Lösungsweg planen:
- seine Vorgehensweise mündlich und schriftlich mitteilen
Sachrechnen – die Ergebnisse interpretieren und bewerten:
- den eigenen Lösungsweg beschreiben und unterschiedliche Lösungswege miteinander vergleichen
Déroulement
1. Bearbeitung der verschiedenen Aufgaben
In Form von Partnerarbeit sollen die Schüler/-innen die einzelnen Aufgaben bearbeiten. Sie dürfen ihre Ergebnisse auf unterschiedlichen Wegen darstellen, sie müssen jedoch immer ihren Lösungsansatz erklären und begründen können.
Die Schüler/-innen bearbeiteten zunächst immer eine Aufgabenstellung und nehmen sich erst dann die nächste Aufgabe, nachdem sie mir ihren Lösungsweg erklären konnten.
Die Schüler/-innen wählen unterschiedliche Wege, um ihre Lösungsvorschläge darzustellen.
2. Präsentation der einzelnen Gruppen
Nachdem die Schüler/innen zu der jeweiligen Fragestellung ihren Rechenweg den anderen Schüler/innen vorgestellt haben, werden im Plenum die verschiedenen Lösungswege diskutiert und eventuelle Denkfehler von den jeweiligen Schüler/-innen erkannt und verbessert.
Observations
Die Schüler arbeiteten intensiv am Lerngegenstand und ließen sich kaum davon abbringen, die Lösungen zu finden. Dies lässt u.a. auf eine hohe Motivation der Schüler/-innen schließen.
Es war sehr still im Raum, so dass ein ruhiges Arbeitsklima herrschte.
Schülerproduktionen
- Vor einem Aufzug stehen 19 Personen. Es dürfen immer 6 Personen mitfahren.

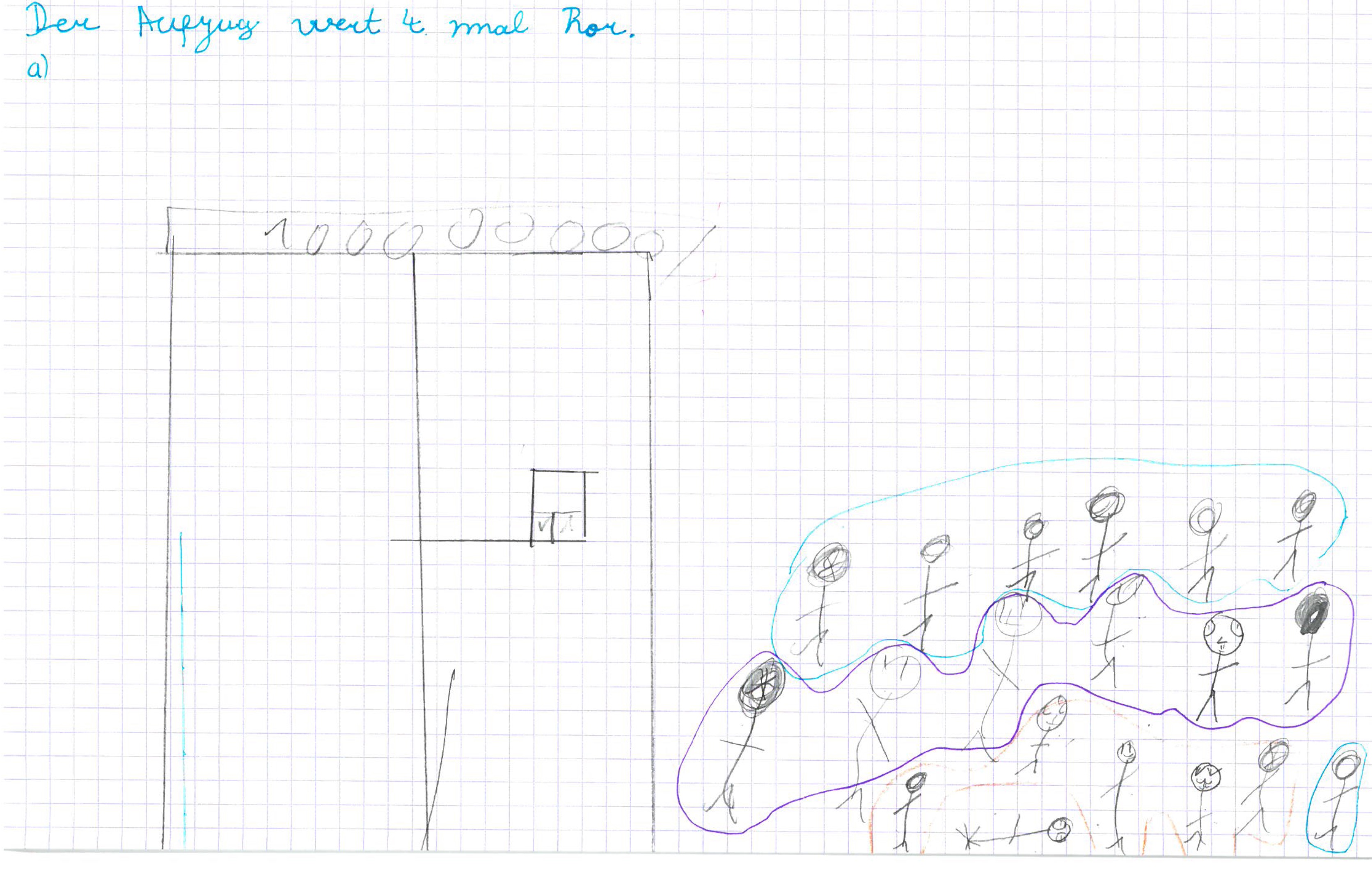

- Felix, Lena und Tim teilen sich 5 Tafeln Schokolade auf.
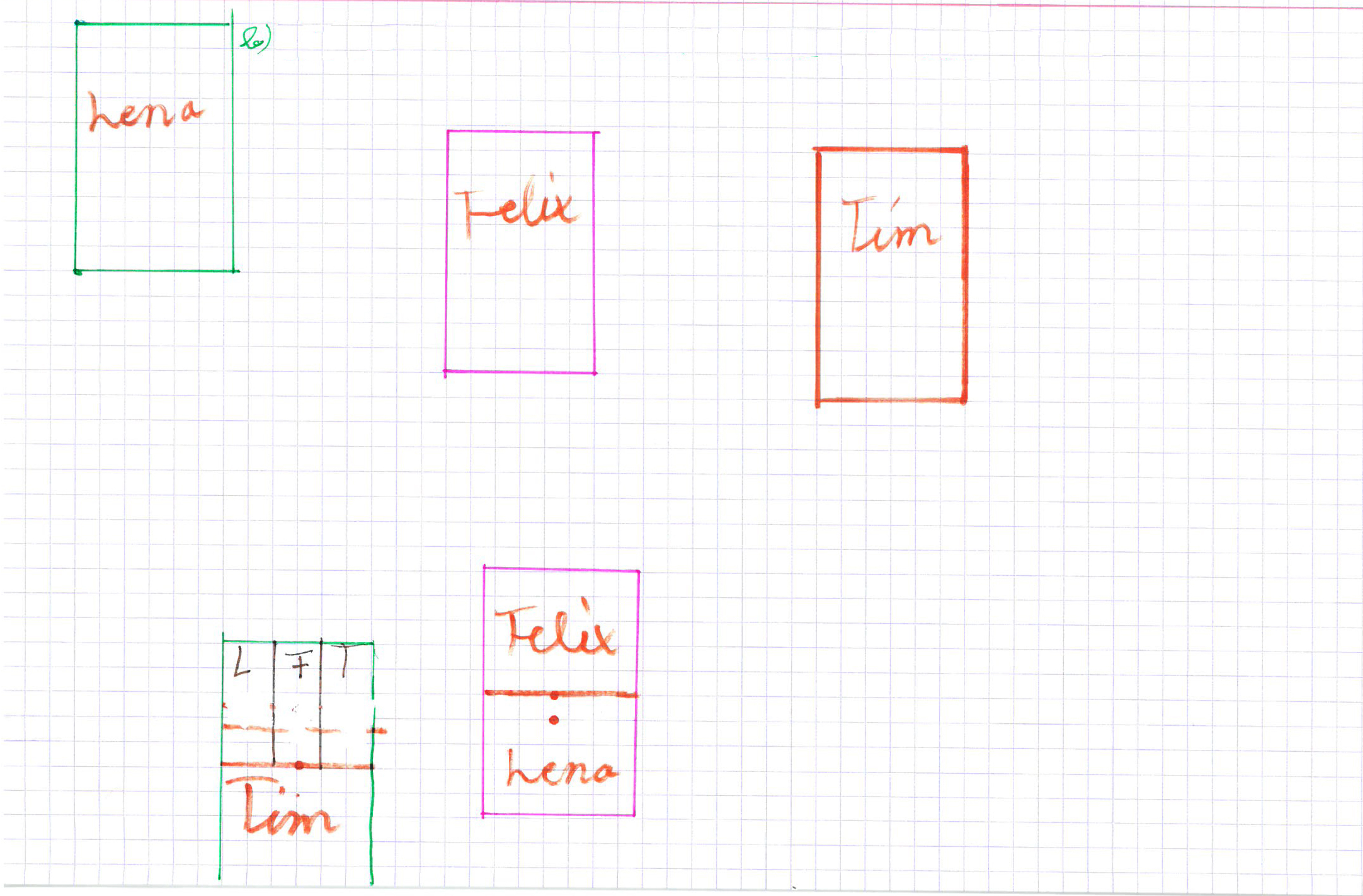
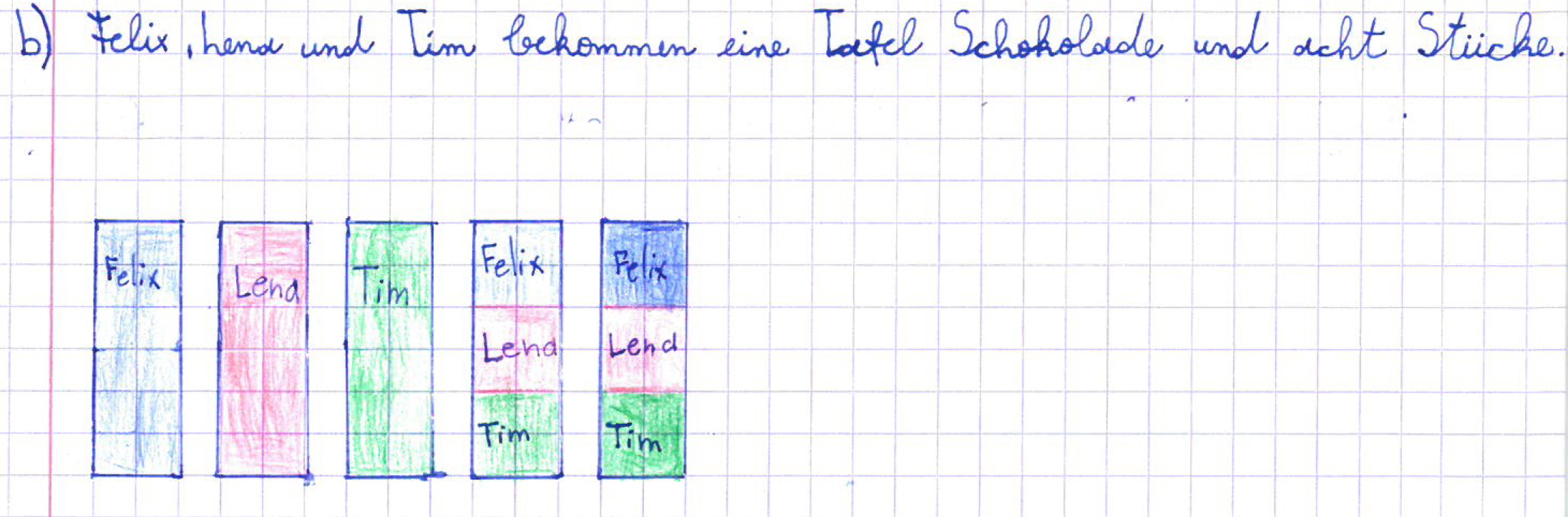
- 4 Freunde helfen einer Nachbarin bei der Gartenarbeit. Sie bekommen dafür eine Packung mit 6 Schokoriegeln.
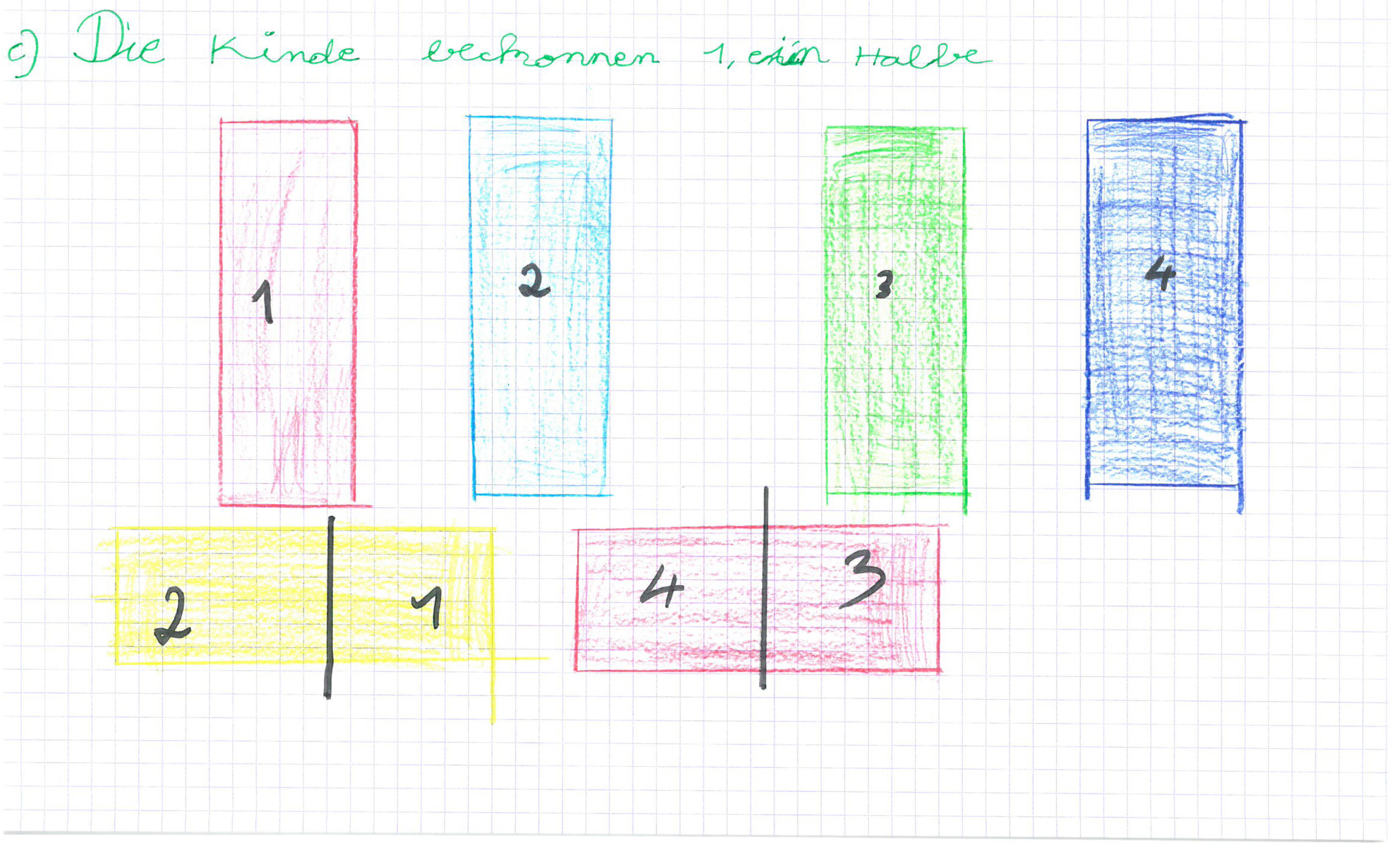

Was gilt es zu beachten?
Die Begleitung der einzelnen Gruppen benötigt eine gute Zeiteinteilung und muss im Voraus geplant sein.
Hypothèses
Wie sind diese Ergebnisse zu erklären?
- Dadurch, dass ich im Vorfeld nicht die Division mit Rest eingeführt habe, waren die Schüler/-innen nicht beeinflusst. Das Ergebnis der Aktivität war somit offen und die Schüler/-innen sind durch ihre Erfahrungen aus ihrem Alltag lösungsorientiert an die Aufgaben herangegangen. Manche Schüler/-innen haben den Bezug zu der Kommaschreibweise von Geldbeträgen gezogen und haben ihre Ergebnisse zum Teil mündlich in Dezimalzahlen wiedergegeben.
- Die Diskussion im Plenum ermöglichte den Schüler/-innen über die verschiedenen Lösungswege zu diskutieren und zu reflektieren. Somit erhielten sie die Möglichkeit das Gelernte weiter zu vertiefen und zu festigen.
| Contexte | Im Anschluss an die Bearbeitung des Einmaleins lernen die Schüler/-innen die Division als Umkehraufgaben kennen. Zudem will ich auch die Divisionsaufgaben mit Rest einführen. Aus dem Grund, dass die Schüler/-innen zunächst keinen Bezug zu solchen arithmetischen Aufgaben herstellen können, habe ich mich dafür entschieden die Thematik anhand von Sachaufgaben einzuführen, welche zum großen Teil einen Bezug zum Alltag der Schüler/-innen nehmen.
|
| Objectifs | Sachrechnen – die Fragestellung einer Sachaufgabe untersuchen und einen Lösungsweg planen:
- seine Vorgehensweise mündlich und schriftlich mitteilen
Sachrechnen – die Ergebnisse interpretieren und bewerten:
- den eigenen Lösungsweg beschreiben und unterschiedliche Lösungswege miteinander vergleichen
|
| Déroulement | 1. Bearbeitung der verschiedenen Aufgaben
In Form von Partnerarbeit sollen die Schüler/-innen die einzelnen Aufgaben bearbeiten. Sie dürfen ihre Ergebnisse auf unterschiedlichen Wegen darstellen, sie müssen jedoch immer ihren Lösungsansatz erklären und begründen können.
Die Schüler/-innen bearbeiteten zunächst immer eine Aufgabenstellung und nehmen sich erst dann die nächste Aufgabe, nachdem sie mir ihren Lösungsweg erklären konnten.
Die Schüler/-innen wählen unterschiedliche Wege, um ihre Lösungsvorschläge darzustellen.
2. Präsentation der einzelnen Gruppen
Nachdem die Schüler/innen zu der jeweiligen Fragestellung ihren Rechenweg den anderen Schüler/innen vorgestellt haben, werden im Plenum die verschiedenen Lösungswege diskutiert und eventuelle Denkfehler von den jeweiligen Schüler/-innen erkannt und verbessert.
|
| Observations | Die Schüler arbeiteten intensiv am Lerngegenstand und ließen sich kaum davon abbringen, die Lösungen zu finden. Dies lässt u.a. auf eine hohe Motivation der Schüler/-innen schließen.
Es war sehr still im Raum, so dass ein ruhiges Arbeitsklima herrschte.
Schülerproduktionen
- Vor einem Aufzug stehen 19 Personen. Es dürfen immer 6 Personen mitfahren.



- Felix, Lena und Tim teilen sich 5 Tafeln Schokolade auf.


- 4 Freunde helfen einer Nachbarin bei der Gartenarbeit. Sie bekommen dafür eine Packung mit 6 Schokoriegeln.


Was gilt es zu beachten?
Die Begleitung der einzelnen Gruppen benötigt eine gute Zeiteinteilung und muss im Voraus geplant sein.
|
| Hypothèses | Wie sind diese Ergebnisse zu erklären?
- Dadurch, dass ich im Vorfeld nicht die Division mit Rest eingeführt habe, waren die Schüler/-innen nicht beeinflusst. Das Ergebnis der Aktivität war somit offen und die Schüler/-innen sind durch ihre Erfahrungen aus ihrem Alltag lösungsorientiert an die Aufgaben herangegangen. Manche Schüler/-innen haben den Bezug zu der Kommaschreibweise von Geldbeträgen gezogen und haben ihre Ergebnisse zum Teil mündlich in Dezimalzahlen wiedergegeben.
- Die Diskussion im Plenum ermöglichte den Schüler/-innen über die verschiedenen Lösungswege zu diskutieren und zu reflektieren. Somit erhielten sie die Möglichkeit das Gelernte weiter zu vertiefen und zu festigen.
|